Question

La

Cu
You can afford monthly deposits of $250 into an account that pays 4.8% compounded
monthly. How long will it be until you have $11,900 to buy a boat?
Att

Answer 1

Explanation:

The formula you need for this is

`A(t)=P(1+(r)/(n))^{nt` where

A(t) is the amount after a certain number of years has gone by,

P is the initial deposit,

r is the interest rate in decimal form,

n is the number of compoundings done per year, and

t is the amount of time in years.

For us,

A(t) = 11900

P is 250

r is .048

n is 12 (there are 12 months in a year)

t is our unknown. Filling in:

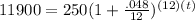`11900=250(1+(.048)/(12))^{(12)(t)` which simplifies a bit to

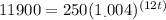`11900=250(1_.004)^{(12t)` . Now we'll divide both sides by 250:

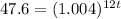`47.6=(1.004)^{12t` and then take the natural log of both sides to bring that t down out front:

`ln(47.6)=ln(1.004)^{12t` and then

ln(47.6) = 12t ln(1.004). Now divide both sides by ln(1.004) to isolate the 12t:

967.6383216 = 12t and divide both sides by `12 to get

t = 80.6 months which is 6.7 years