Answer:
a) the final velocity is 35.75 ft/s
b) The final elevation is 45 ft
Step-by-step explanation:
Given the data in the question;
Weight of object; W = 100 lbf
Change in kinetic energy; ΔE = 500 ft-lb
so
 m
m
 -
-
 m
m
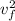 = ΔE
= ΔE
 m
m
 -
-
 m
m
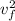 = 500
= 500
multiply both sides by 2
m
 - m
- m
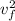 = 1000
= 1000
m(
 -
-
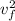 ) = 1000
) = 1000
 -
-
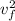 = 1000/m
= 1000/m
 -
-
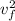 = (1000)(g) / W
= (1000)(g) / W
we know that, acceleration due to gravity g = 9.8 m/s² = 32.18 ft/s²
so we substitute
 -
-
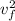 = (1000)(32.18) / 100
= (1000)(32.18) / 100
 -
-
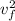 = (1000)(32.18) / 100
= (1000)(32.18) / 100
 -
-
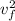 = 32180 / 100
= 32180 / 100
 -
-
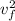 = 321.8
= 321.8
since The initial velocity
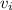 is given to be 40 ft/s;
is given to be 40 ft/s;
(40)² -
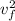 = 321.8
= 321.8
1600 -
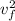 = 321.8
= 321.8
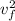 = 1600 - 321.8
= 1600 - 321.8
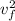 = 1278.2
= 1278.2
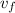 = √1278.2
= √1278.2
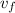 = 35.75 ft/s
= 35.75 ft/s
Therefore, the final velocity is 35.75 ft/s
b)
we know that;
change in potential energy is;
ΔP.E = mg( h
 - h
- h
 )
)
given that; increase in potential energy; ΔP.E = 1500 ft-lbf
and mg = Weight = 100 lbf
we substitute
1500 = 100( h
 - h
- h
 )
)
h
 - h
- h
 = 1500 / 100
= 1500 / 100
h
 - h
- h
 = 15 ft
= 15 ft
given that, elevation of the object; h
 = 30 ft
= 30 ft
h
 - 30 ft = 15 ft
- 30 ft = 15 ft
h
 = 15 ft + 30 ft
= 15 ft + 30 ft
h
 = 45 ft
= 45 ft
Therefore, The final elevation is 45 ft