Question

Statements that are true for a cylinder with radius r and height h.

Doubling r doubles the volume.

Doubling r quadruples the volume.

Doubling h doubles the volume.

Doubling h quadruples the volume.

Doubling h and r quadruples the volume.

Answer 1

Only the second and third statements are correct:

Doubling r quadruples the volume.

Doubling h doubles the volume.

Explanation:

The volume of a cylinder is given by:

`\displaystyle V=\pi r^2h`

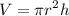
We can go through each statement and examine its validity.

Statement 1)

If the radius is doubled, our new radius is now 2r. Hence, our volume is:

`\displaystyle V=\pi (2r)^2h=4\pi r^2h`

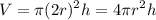
So, compared to the old volume, the new volume is quadrupled the original volume.

Statement 1 is not correct.

Statement 2)

Using the previous reasonsing, Statement 2 is correct.

Statement 3)

If the height is doubled, our new height is now 2h. Hence, our volume is:

`V=\pi r^2(2h)=2\pi r^2h`

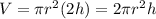
So, compared to the old volume, the new volume has been doubled.

Statement 3 is correct.

Statement 4)

Statement 4 is not correct using the previous reasonsing.

Statement 5)

Doubling the radius results in 2r and doubling the height results in 2h. Hence, the new volume is:

`V=\pi (2r)^2(2h)=\pi (4r^2)(2h)=8\pi r^2h`

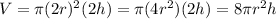
So, compared to the old volume, the new volume is increased by eight-fold.

Statement 5 is not correct.