Answer:
a) probability that any individual student has a flu shot is 0.30
b) The probability that more than 30 students have had flu shots is 0.1038
c) the probability that 20 or fewer students have had shots is 0.1314
Explanation:
Given the data in the question;
Number of students n = 84
student health clinic reports that only 30% of students got a flu shot this year;
p = 30% = 0.30
now,
pn = 0.30 × 84 = 25.2 ( > 10 )
qn = (1-p)n = (1-0.30)84 = 0.70 × 84 = 58.8 ( > 10 )
Criterion for approximation of the binomial distribution is satisfied since both pn and qn are greater than 10.
hence, Normal distribution will have;
mean μ = np = 0.30 × 84 = 25.2
standard deviation σ = √( npq )
= √( 84 × 0.30 × 0.70 )
= √17.64
standard deviation σ = 4.2
a) the probability that any individual student has a flu shot
student health clinic reports that only 30% of students got a flu shot this year
p = 30% = 0.30
Therefore, probability that any individual student has a flu shot is 0.30
b) The probability that more than 30 students have had flu shots
P(X > 30)
we use real time limits to determine probability from binomial distribution,
hence upper limit will be 30.5
Z = (X - np) / √( npq )
Z = ( 30.5 - 25.2 ) / 4.2
Z = 5.3 / 4.2
Z = 1.26
from normal distribution table
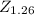 = 0.1038
= 0.1038
Therefore, The probability that more than 30 students have had flu shots is 0.1038
c) the probability that 20 or fewer students have had shots;
P( X ≤ 20 )
upper limit will be 20.5
Z = (X - np) / √( npq )
Z = ( 20.5 - 25.2 ) / 4.2
Z = -4.7 / 4.2
Z = -1.12
from normal distribution table
 = 0.1314
= 0.1314
Therefore, the probability that 20 or fewer students have had shots is 0.1314