Question

Assume that you want to construct a box with a square base (closed top) and a volume of 1000 cm3 . Find the dimensions of the box to minimize the surface area of the box.

Answer 1

`x=10\sqrt[3]{2}`

Explanation:

The Volume of a box with a square base

x by x cm and height h cm is

V =x^2h

The amount of material used is directly proportional to the surface area, so we will minimize the amount of material by minimizing the surface area.

The surface area of the box described is

A = x ^2 +4 x h

We need

A as a function of x alone, so we'll use the fact that

V= x^2h = 1000 cm^3

This imples
`h=(1000)/(x^2)`

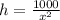
This makes

`A= x^2 + 4x(1000/x^2)\\A= x^2+4000/x`

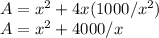
Differentiating A w.r.t. x

`A' = 2x-4000/x^2`

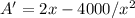
Now, A'=0

`x=10\sqrt[3]{2}`

Therefore, minimum value x =
`x=10\sqrt[3]{2}`