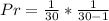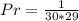Answer:

Explanation:
Given

Required
Probability of selecting 2 toys of different types
From the question, we understand that all toys are different i.e. 1 of each type.
And the selection is without replacement;
So, after the first toy is selected; there are n - 1 toys left.
So, the probability is:
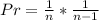
Substitute