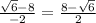Question

RATIONALIZE THE
Denominator and
simplify

Answer 1

`(8-√(6) )/(2)`

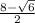
Explanation:

To rationalize the denominator, we need to multiply both the numerator and denominator by the conjugate of the denominator, which in this is 2 - √6.

We can write the expression:

`(3√(6)+5 )/(2+√(6)) *(2-√(6))/(2-√(6) )`

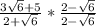
We can use the special product of the difference of squares to simplify the denominator:

`(2 + √(6))(2-√(6)) = 2^2 - (√(6))^2 =4 - 6 = -2`

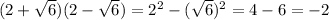
We can use distributive for the numerator:

`(3√(6)+5)(2-√(6))=6√(6) -18+ 10-5√(6) =√(6) -8`

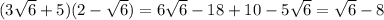
Now we can rewrite the fraction:

`(√(6)-8 )/(-2) =(8-√(6) )/(2)`