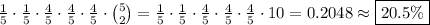Question

There are 5 questions on a multiple choice exam, each with five possible answers. If a student guesses on all five questions, what is the probability the student gets two questions correct? Express your answer as a percent rounded to the nearest tenth.

3.8%

18.7%

20.5%

16.9%

Answer 1

`20.5\%`

Explanation:

Let's write out a case for two specific questions being correct and the rest being incorrect:

`(1)/(5)\cdot (1)/(5)\cdot (4)/(5)\cdot (4)/(5)\cdot (4)/(5)`,

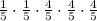The
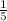`(1)/(5)` represents the chances of getting the question correct, as there are 5 answers and 1 correct answer choice.

The
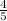`(4)/(5)` represents the chances of getting the question incorrect, as there are 5 answers and 4 incorrect answer choices.

The equation above does show the student getting two answers correct and three answers incorrect, but it only shows one possible case of doing so.

We can choose any two of the five questions to be the ones the student gets correct. Therefore, we need to multiply this equation by the number ways we can choose 2 from 5 (order doesn't matter):
`\binom{5}{2}=10`.

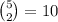Therefore, the probability the student gets two questions correct is:

`(1)/(5)\cdot (1)/(5)\cdot (4)/(5)\cdot (4)/(5)\cdot (4)/(5)\cdot \binom{5}{2}=(1)/(5)\cdot (1)/(5)\cdot (4)/(5)\cdot (4)/(5)\cdot (4)/(5)\cdot 10=0.2048\approx \boxed{20.5\%}`