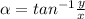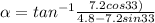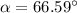Answer:
a)
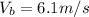
b)
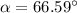
Step-by-step explanation:
From the question we are told that:
Width of river
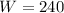
River speed
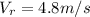
Boat speed
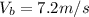
Boat Direction
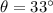
Generally the equation for Boat Velocity Vector is mathematically given by
By Resolving Co-Planar forces
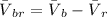

Therefore

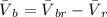
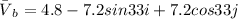
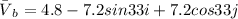
Therefore Magnitude of Boat velocity is
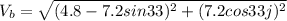
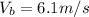
b)
Generally the equation for Direction of the boat's velocity is mathematically given by