Answers: First Quadrant and Fourth Quadrant
======================================================
Step-by-step explanation:
Let
be the two complex numbers.
Multiply them out to see what we get
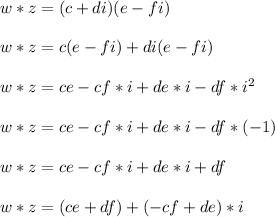
The result we get is in the form a+bi where
- a = ce+df = real part
- b = -cf+de = imaginary part
Recall that any complex number of the form a+bi can be plotted on the xy plane with 'a' being treated as the x coordinate and b as the y coordinate. In short, the location of a+bi is at the point (a,b)
With c,d,e,f being positive, this means ce and df are positive, and a = ce+df is also positive.
This places the result of wz in either the first or fourth quadrants (the northeast or southeast quadrants respectively), due to the positive x coordinate.
We don't have enough info to determine whether b = -cf+de is positive or not. So that's why we can't nail down the precise quadrant of wz
If b > 0, then wz is in quadrant 1
If b < 0, then wz is in quadrant 4