Question

Express the following in the form a +bi, where a and b are real numbers:


`√(24 + 10i)`
​

Answer 1

Answer: 5+i

Another accepted answer is -5-i, but if your teacher wants only one answer, then I'd go for 5+i

======================================================

Work Shown:

`√(24+10i) = a+bi\\\\\left(√(24+10i)\right)^2 = (a+bi)^2\\\\24+10i = a^2+2abi+b^2i^2\\\\24+10i = a^2+2abi+b^2(-1)\\\\24+10i = a^2+2abi-b^2\\\\24+10i = (a^2-b^2)+(2ab)i\\\\`

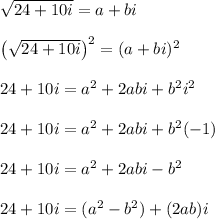
Equating terms, we have this system

`\begin{cases}24 = a^2-b^2\ \text{.... real terms}\\10 = 2ab\ \text{.... imaginary terms}\end{cases}`

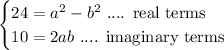
Solve the second equation for b to get b = 5/a

Plug that into the first equation to solve for 'a'

`24 = a^2-b^2\\\\24 = a^2-\left((5)/(a)\right)^2\\\\24 = a^2-(25)/(a^2)\\\\24a^2 = a^4-25\\\\0 = a^4-24a^2-25\\\\a^4-24a^2-25 = 0\\\\(a^2-25)(a^2+1) = 0\\\\(a-5)(a+5)(a^2+1) = 0\\\\`

Setting each factor equal to zero would lead to...

• a-5 = 0 solves to a = 5
• a+5 = 0 solves to a = -5
• a^2+1 = 0 solves to a = i and a = -i

We're told that 'a' is a real number, so we ignore the solutions "a = i and a = -i". The only possible solutions are a = 5 and a = -5

If a = 5, then,

b = 5/a = 5/5 = 1

So

`√(24+10i) = a+bi = 5+1i = 5+i`

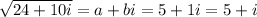
or in short,

`√(24+10i) = 5+i`

-----------------

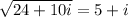
If a = -5, then b = 5/a = 5/(-5) = -1

So it's very possible that we could also say

`√(24+10i) = -5-i\\\\`

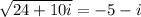
If you wanted to combine the two we would use the plus/minus notation like so

`√(24+10i) = \pm(5+i)\\\\`

This is due to (5+i)^2 and (-5-i)^2 both having the same result of 24+10i. Hence the plus/minus. If your teacher wants one answer only, then I'd go for 5+i, as we could consider it a "principal" square root in a sense.