Answer:
 whenever
whenever
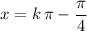 radians, where
radians, where
 could be any integer (
could be any integer (
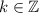 , which includes positive whole numbers, negative whole numbers, and zero.)
, which includes positive whole numbers, negative whole numbers, and zero.)
Explanation:
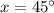 (as in isoscele right triangles) would ensure that
(as in isoscele right triangles) would ensure that
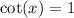 . Since cotangent is an odd function,
. Since cotangent is an odd function,
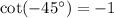 .
.
Equivalently, when the angles are expressed in radians,
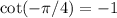 .
.
The cycle of cotangent is
 (or equivalently,
(or equivalently,
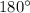 .) Therefore, if
.) Therefore, if
 represents an integer, adding
represents an integer, adding
 to the input to cotangent would not change the output. In other words:
to the input to cotangent would not change the output. In other words:
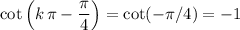 .
.
Hence,
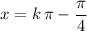 would be a solution to
would be a solution to
 whenever
whenever
 is an integer.
is an integer.
Since
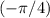 is the only solution to this equation in the period
is the only solution to this equation in the period
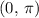 , all real solutions to this equation would be in the form
, all real solutions to this equation would be in the form
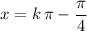 (where
(where
 is an integer.)
is an integer.)