Question

A container of oxygen gas is at STP. If this sample is put into an oven at 280 C, what would its pressure be, in atmospheres?

Answer 1

Explanation:

Step 1:

Data obtained from the question. This include the following:

Initial pressure (P1) = 1atm

Initial temperature (T1) = 0°C = 0°C + 273 = 273K

Final temperature (T2) = 280°C = 280°C + 273 = 553K

Final pressure (P2) =...?

Step 2:

Determination of the new pressure of the gas.

Since the volume of the gas is constant, the following equation:

P1/T1 = P2/T2

will be used to obtain the pressure. This is illustrated below:

P1/T1 = P2/T2

1/273 = P2 / 553

Cross multiply

273x P2 = 553

Divide both side by 273

P2 = 553/273

P2 = 2.03atm

Therefore, the new pressure of the gas will be 2.03atm

Answer 2

`\boxed {\boxed {\sf P_2=2.03 \ atm}}`

Step-by-step explanation:

We are concerned with the variables of temperature and pressure, so we use Gay-Lussac's Law, which states the temperature of a gas is directly proportional to the pressure. The formula is:

`(P_1)/(T_1)=(P_2)/(T_2)`

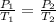
We know that the container of gas begins at standard temperature and pressure (STP). This is 1 atmosphere of pressure and 273 Kelvin.

`\frac { 1 \ atm}{ 273 \ K} = (P_2)/(T_2)`

We know the gas is put into an oven at 280 degrees Celsius. We can convert this to Kelvin.

• K= °C + 273.15
• K= 280 +273.15
• K= 553.15

`\frac { 1 \ atm}{ 273 \ K} = (P_2)/(553.15 \ K)`

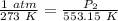
We are solving for the new pressure, so we must isolate the variable P₂. It is being divided by 553.15 Kelvin. The inverse of division is multiplication, so we multiply both sides by 553.15 K

`553.15 \ K *\frac { 1 \ atm}{ 273 \ K} = (P_2)/(553.15 \ K) * 553.15 \ K`

`553.15 \ K *\frac { 1 \ atm}{ 273 \ K}= P_2`

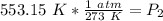
The units of Kelvin cancel.

`553.15 *\frac { 1 \ atm}{ 273 }= P_2`

`2.02619047619 \ atm = P_2`

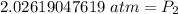
Rounded to the nearest hundredth:

`2.03 \ atm \approx P_2`

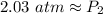
The new pressure is approximately 2.03 atmospheres.