Answer:
y =
 x + 3
x + 3
Explanation:
As shown in the graph, the line is a straight line. Therefore, the general equation of a straight line can be employed to derive the equation of the line.
The general equation of a straight line is given by:
y = mx + c or -------------(i)
y - y₁ = m(x - x₁) -----------------(ii)
Where;
y₁ is the value of a point on the y-axis
x₁ is the value of the same point on the x-axis
m is the slope of the line
c is the y-intercept of the line.
Equation (i) is the slope-intercept form of a line
Steps:
(i) Pick any two points (x₁, y₁) and (x₂, y₂) on the line.
In this case, let;
(x₁, y₁) = (0, 3)
(x₂, y₂) = (4, -2)
(ii) With the chosen points, calculate the slope m given by;
m =

m =
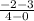
m =

(iii) Substitute the first point (x₁, y₁) = (0, 3) and m =
 into equation (ii) as follows;
into equation (ii) as follows;
y - 3 =
 (x - 0)
(x - 0)
(iv) Solve for y from (iii)
y - 3 =
 x
x
y =
 x + 3 [This is the slope intercept form of the line]
x + 3 [This is the slope intercept form of the line]
Where the slope is
 and the intercept is 3
and the intercept is 3