Answer:
She needs an annual interest rate of 7.54%.
Explanation:
Compound interest:
The compound interest formula is given by:
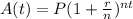
Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per year and t is the time in years for which the money is invested or borrowed.
She figures that this will cost a total of $25,750.
This means that
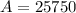 .
.
Sandra already has $21,400 saved up
This means that
 .
.
Semianually compunding, 2.5 years.
This means that
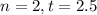
What interest rate?
We have to find r. So
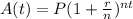
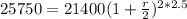
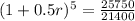
![\sqrt[5]{(1 + 0.5r)^5} = \sqrt[5]{(25750)/(21400)}](https://img.qammunity.org/2022/formulas/mathematics/college/8wub3bvd5qbfru4w7xhlntzxxjuag7dt1p.png)
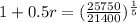
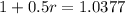
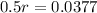
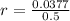
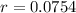
0.0754*100% = 7.54%
She needs an annual interest rate of 7.54%.