Question

A boat travels at 15 m/s in a direction 45° east of north for an hour. The boat then turns and travels at 18 m/s in a

direction 5° north of east for an hour.
What is the magnitude of the boat's resultant velocity? Round your answer to the nearest whole number.
I mis
What is the direction of the boat's resultant velocity? Round your answer to the nearest whole degree.
north of east
Done
Intro

Answer 1

v = 31 m, / s; θ = 1 north- east

Step-by-step explanation

One of the easiest ways to solve these problems is to work with the components of vectors.

Let's set a reference system where the x axis coincides with the West - East direction

Let's use trigonometry

cos 45 = v₁ₓ / v₁

sin 45 = v_{1y} / v₁

v₁ₓ = v1 cos 45

v_{1y} = v₁₁ sin 5

v₁ₓ = 15 cos 45 = 10.6 m / s

v _{1y} = 15 sin 45 = 10.6 m / s

sin 5 = v₂ₓ / v₂

cos 5 = v_{2y} / v₂

v₂ₓ = v2 sin 5

v_{2y}= v2 sin 5

v₂ₓ = 18 sin 5 = 1.569 m / s

v_{2yₓ} = 18 cos 5 = 17.93 m / s

Let's look for the speed in each axis

vₓ = v₁ₓ + v₂ₓ

vx = 10.6 + 1.569

vx = 12.17 m / s

v_y = v_{1y} + v_{2y}

v_y = 10.6 + 17.93

v_y = 28.53 m / s

to find the velocity let's use the Pythagorean theorem

v =
`√(v_x^2 +v_2^2 )`

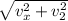
v = √ (12.17² + 28.53²)

v = 31.02 m / s

approaching the nearest ether

v = 31 m / s

b) we use trigonometry

tan θ = vy / vx

θ = tan -1

θ = tan vy / vx

θ = tan-1 17.93 / 12.17

θ= 1.47

the closeΕst integer is

θ = 1 north- east