I'll interpret the given statement as
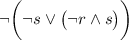
where
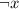 means "not x",
means "not x",
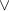 means "or", and
means "or", and
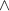 means "and".
means "and".
If r is false, then
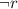 is true.
is true.
s is given to be false, so
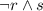 (basically "true and false") is false.
(basically "true and false") is false.
If s is false, then
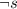 is true.
is true.
Then
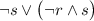 (i.e. "true or false") is true.
(i.e. "true or false") is true.
Take the negation of that and you end up with a false statement.
If you intended "~r < s" to mean something like "not r is implied by s", so the original statement is actually
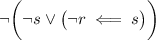
then
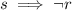 is true because s is false. Then
is true because s is false. Then
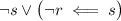 is still true, so the statement still ends up being false.
is still true, so the statement still ends up being false.