Question

Please help with math questions

Answer 1

60 is the answer I hope this is right

Answer 2

See answers below

Explanation:

Problem 1

Recall that
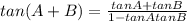`tan(A+B)=(tanA+tanB)/(1-tanAtanB)` and that
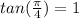`tan((\pi)/(4))=1`. Using these two facts, we can rewrite the expression:

`(1+tanx)/(-1+tanx)\\\\-(1+tanx)/(1-tanx)\\ \\-(tan((\pi)/(4))+tanx)/(1-tan((\pi)/(4))tan(x))\\ \\-tan(x+(\pi)/(4))\\ \\tan((3\pi)/(4)-x)`

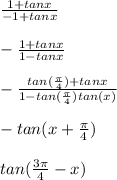
Hence, the first choice is correct

Problem 2

`cos((x)/(2))=√(3)-cos((x)/(2))\:;\: 0\leq x < 360^\circ\\\\2cos((x)/(2))=√(3)\\ \\cos((x)/(2))=(√(3))/(2)\\\\(x)/(2)=(\pi)/(6)+2\pi n,(11\pi)/(6)+2\pi n\\ \\ x=(\pi)/(3)+4\pi n,(11\pi)/(3)+4\pi n\\ \\ x=60^\circ+720n^\circ, 660^\circ+720n^\circ\\\\x=60^\circ`

It's helpful to use the unit circle to solve these kinds of problems. Therefore, the third answer is correct.

Problem 3

Because
`sin\theta=-(5)/(13)` and our parameters are
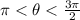`\pi < \theta < (3\pi)/(2)`, the triangle must be in Quadrant III where
`sin\theta < 0` and
`cos\theta < 0`.

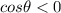You may recall the double angle formula
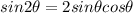`sin2\theta=2sin\theta cos\theta`. We can find
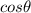`cos\theta` using
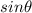`sin\theta` with the Pythagorean Identity
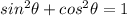`sin^2\theta+cos^2\theta=1` keeping our parameters in mind:

`sin^2\theta+cos^2\theta=1\\\\(-(5)/(13))^2+cos^2\theta=1\\ \\(25)/(169)+cos^2\theta=1\\ \\cos^2\theta=(144)/(169)\\ \\cos\theta=-(12)/(13)`

Thus,
`sin2\theta=2sin\theta cos\theta=2(-(5)/(13))(-(12)/(13))=2((60)/(169))=(120)/(169)`, which means the third option is correct.