Question

If dy/dx = ysec^2(x) and y= 5 when x = 0, then y=?

А. e^tanx +4
B. e^tanx +5
C. 5e^tanx
D. tanx + 5
E. tanx + 5e^x

Answer 1

C.
`\displaystyle y = 5e^(tan(x))`

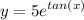
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Functions
• Function Notation
• |Absolute Values|
• Anything to the 0th power is 1

Algebra II

• Logarithms and Natural logs
• Euler's number e

Calculus

Derivatives

Derivative Notation

Trig Derivatives

Differential Equations

• Separation of variables
• General and particular solutions

Antiderivatives - Integration

Integration Constant C

Trig Integration

Logarithmic Integration

Explanation:

Step 1: Define

Identify

`\displaystyle (dy)/(dx) = ysec^2(x)`

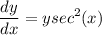
x = 0, y = 5

Step 2: Rewrite Differential

Separation of variables

1. [Division Property of Equality] Isolate y terms together:
   `\displaystyle (1)/(y)(dy)/(dx) = sec^2(x)`
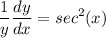
2. [Multiplication Property of Equality] Isolate x terms together:
   `\displaystyle (1)/(y)dy = sec^2(x)dx`

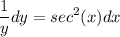
Step 3: Find General Solution

1. [Equality Property] Integrate both sides:
   `\displaystyle \int {(1)/(y)} \, dy = \int {sec^2(x)} \, dx`
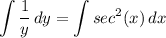
2. [1st Integral] Integrate [Logarithmic Integration]:
   `\displaystyle ln|y| = \int {sec^2(x)} \, dx`
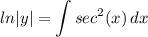
3. [2nd Integral] Integrate [Trig Integration]:
   `\displaystyle ln|y| = tan(x) + C`
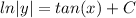
4. [Equality Property] e both sides:
   `\displaystyle e^(ln|y|) = e^(tan(x) + C)`
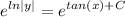
5. Simplify:
   `\displaystyle |y| = Ce^(tan(x))`
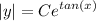
6. Rewrite:
   `\displaystyle y = \pm Ce^(tan(x))`

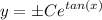
Step 4: Find Particular Solution

1. Substitute in variables [Function]:
   `\displaystyle |5| = Ce^(tan(0))`
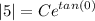
2. Evaluate absolute value:
   `\displaystyle 5 = Ce^(tan(0))`
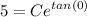
3. Evaluate trig:
   `\displaystyle 5 = Ce^0`
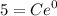
4. Evaluate exponent:
   `\displaystyle 5 = C(1)`
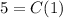
5. Multiply:
   `\displaystyle 5 = C`
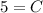
6. Rewrite:
   `\displaystyle C =5`
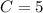
7. Substitute in C [General Solution]:
   `\displaystyle y = 5e^(tan(x))`

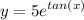
∴ Our answer is C.

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Differential Equations

Book: College Calculus 10e