Question

Find sin(a+B)

cos a = 5/13, with a in quadrant I
tanB = 4/3 with B in quadrant 4.
Give exact answer, not decimal approximation.

sin(a+B)=

Answer 1

Cos A=5/13

we have

Cos² A=
`1-Sin ²A`

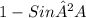
25/169=1-Sin²A

sin²A=1-25/169

sin²A=144/169

Sin A=
`√(144/169)=12/13`

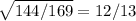
again

Tan B=4/3

P/b=4/3

p=4

b=3

h=
`√(3²+4²)=5`

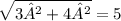
Now

Sin B=p/h=4/5

in IV quadrant sin angle is negative so

Sin B=-4/5

CosB=b/h=3/5

Now

Sin(A+B):sinAcosB+CosAsinB

now

substitute value

Sin(A+B):12/13*3/5+5/13*(-4/5)=36/65-4/13

=16/65 is a required answer