Question

The third-degree Taylor polynomial about x = 0 of In(1 - x) is

Answer 1

`\displaystyle P_3(x) = -x - (x^2)/(2) - (x^3)/(3)`

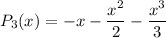
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Functions
• Function Notation

Calculus

Derivatives

Derivative Notation

Derivative Rule [Quotient Rule]:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

MacLaurin/Taylor Polynomials

• Approximating Transcendental and Elementary functions
• MacLaurin Polynomial:
  `\displaystyle P_n(x) = (f(0))/(0!) + (f'(0))/(1!)x + (f''(0))/(2!)x^2 + (f'''(0))/(3!)x^3 + ... + (f^((n))(0))/(n!)x^n`
• Taylor Polynomial:
  `\displaystyle P_n(x) = (f(c))/(0!) + (f'(c))/(1!)(x - c) + (f''(c))/(2!)(x - c)^2 + (f'''(c))/(3!)(x - c)^3 + ... + (f^((n))(c))/(n!)(x - c)^n`

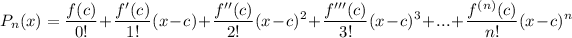
Explanation:

*Note: I will not be showing the work for derivatives as it is relatively straightforward. If you request for me to show that portion, please leave a comment so I can add it. I will also not show work for elementary calculations.

Step 1: Define

Identify

f(x) = ln(1 - x)

Center: x = 0

n = 3

Step 2: Differentiate

1. [Function] 1st Derivative:
   `\displaystyle f'(x) = (1)/(x - 1)`
2. [Function] 2nd Derivative:
   `\displaystyle f''(x) = (-1)/((x - 1)^2)`
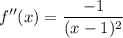
3. [Function] 3rd Derivative:
   `\displaystyle f'''(x) = (2)/((x - 1)^3)`

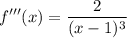
Step 3: Evaluate Functions

1. Substitute in center x [Function]:
   `\displaystyle f(0) = ln(1 - 0)`
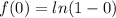
2. Simplify:
   `\displaystyle f(0) = 0`
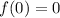
3. Substitute in center x [1st Derivative]:
   `\displaystyle f'(0) = (1)/(0 - 1)`
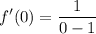
4. Simplify:
   `\displaystyle f'(0) = -1`
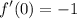
5. Substitute in center x [2nd Derivative]:
   `\displaystyle f''(0) = (-1)/((0 - 1)^2)`
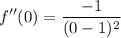
6. Simplify:
   `\displaystyle f''(0) = -1`
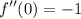
7. Substitute in center x [3rd Derivative]:
   `\displaystyle f'''(0) = (2)/((0 - 1)^3)`
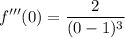
8. Simplify:
   `\displaystyle f'''(0) = -2`

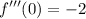
Step 4: Write Taylor Polynomial

1. Substitute in derivative function values [MacLaurin Polynomial]:
   `\displaystyle P_3(x) = (0)/(0!) + (-1)/(1!)x + (-1)/(2!)x^2 + (-2)/(3!)x^3`
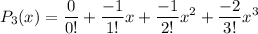
2. Simplify:
   `\displaystyle P_3(x) = -x - (x^2)/(2) - (x^3)/(3)`

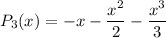
Topic: AP Calculus BC (Calculus I/II)

Unit: Taylor Polynomials and Approximations

Book: College Calculus 10e