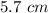Question

A rectangle has an area of 19.38 cm2. When both the length and width of the rectangle are increased by 1.50 cm, the area of the rectangle becomes 35.28 cm2. Calculate the length of the longer of the two sides of the initial rectangle.

Answer 1

Answer:
`5.7\ cm`

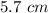
Explanation:

Given

Rectangle has an area of
`19.38\ cm^2`

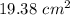
Suppose rectangle length and width are
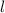`l` and
`w`

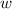
If each side is increased by
`1.50\ cm`

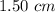
Area becomes
`A_2=35.28\ cm^2`

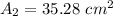
We can write

`\Rightarrow lw=19.38\quad \ldots(i)\\\\\Rightarrow (l+1.5)(w+1.5)=35.28\\\Rightarrow lw+1.5(l+w)+1.5^2=35.28\\\text{use (i) for}\ lw\\\Rightarrow 19.38+1.5(l+w)=35.28-2.25\\\Rightarrow l+w=9.1\quad \ldots(ii)`

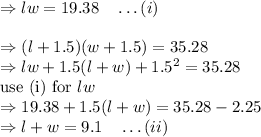
Substitute the value of width from (ii) in equation (i)

`\Rightarrow l(9.1-l)=19.38\\\Rightarrow l^2-9.1l+19.38=0\\\\\Rightarrow l=(9.1\pm√((-9.1)^2-4(1)(19.38)))/(2* 1)\\\\\Rightarrow l=(9.1\pm√(5.29))/(2)\\\\\Rightarrow l=(9.1\pm2.3)/(2)\\\\\Rightarrow l=3.4,\ 5.7`

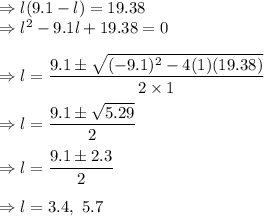
Width corresponding to these lengths

`w=5.7,\ 3.4`

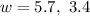
Therfore, we can write the length of the longer side is
`5.7\ cm`