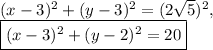Question

HELP DUE IN 15 MINS!

The center of a circle is (3, 2) and a point on the circle is (5, -2). Find the radius and write the equation for the circle.

Answer 1

Radius:
`2√(5)`

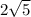
Equation of circle:
`(x-3)^2+(y-2)^2=20`

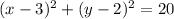
Explanation:

The radius of a circle is equal to the distance between the center of the circle and any point on the circle. Therefore, we have:

`r=√((5-3)^2+(2-(-2))^2),\\r=√(2^2+4^2),\\r=√(20)=\boxed{2√(5)}`

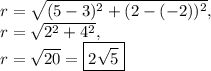
The equation of a circle with radius
`r` and center
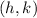`(h, k)` is given by:

`(x-h)^2+(y-k)^2=r^2`.

What we know:

• radius of
  `2√(5)`
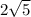
• center at
  `(3, 2)`

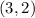
Substituting known values, we get:

`(x-3)^2+(y-3)^2=(2√(5))^2,\\\boxed{(x-3)^2+(y-2)^2=20}`

Answer 2

r =
`2√(5)`

`(x - 3)^(2) + ( y - 2)^(2) = 20`

Is this a live test question or a homework question?

Explanation:

the radius is the distance between (3, 2) and (5, -2)

`r^(2)` =
`{(3 - 5)^(2) + (2 + 2)^(2) }`

=
`(-2)^(2) + 4^(2)`

= 4 + 16 = 20

r =
`√(20 ) = 2√(5)`

Equation of circle:
`(x - 3)^(2) + ( y - 2)^(2) = 20`