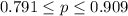Question

Assume that a sample is used to estimate a population proportion p. Find the 99.9% confidence interval for a sample of size 247 with 85% successes. Enter your answer as a tri-linear inequality using decimals (not percents) accurate to three decimal places

Answer 1

Answer:
`0.791\leq p\leq0.909`

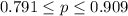
Explanation:

The confidence interval for the population proportion is given by:-

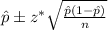`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`, where
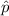`\hat{p}`= sample proportion, n =sample space , z* = critical z-value.

As per given, we have

`n = 247`

`\hat{p}=0.85`

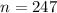
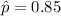
Critical value for 99.9% confidence = 2.576

The required confidence interval will be:

`0.85-2.576\sqrt{(0.85*0.15)/(247)}\leq p\leq 0.85+2.576\sqrt{(0.85*0.15)/(247)}\\\\\Rightarrow\ 0.85-(0.058526)\leq p \leq0.85+(0.058526)\\\\\Rightarrow\ 0.791474\leq p\leq0.908526\approx0.791\leq p\leq0.909`

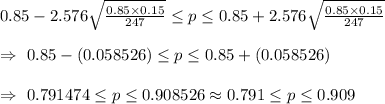
The required confidence interval:
`0.791\leq p\leq0.909`