Question

If a second ball were dropped from rest from height ymax, how long would it take to reach the ground

Answer 1

`(b)\ t_1 - t_0`

`(d)\ t_2 - t_1`

`(e)\ (t_2 - t_0)/(2)`

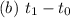
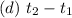
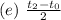
Step-by-step explanation:

Given

See attachment for complete question

Required

How long to reach the ground from the maximum height

First, calculate the time of flight (T)

`T =t_2 - t_0`

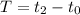
The time taken (t) from maximum height to the ground is:

`t = (1)/(2)T`

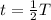
So, we have:

`t = (t_2 - t_0)/(2)`

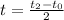
Another representation is:

At ymax, the time is: t1

On the ground, the time is t2

The difference between these times is the time taken.

So;

`t = t_2 - t_1`

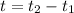
Since air resistance is to be ignored, then

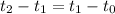`t_2 - t_1 = t_1 - t_0` --- i.e. time to reach the maximum height from the ground equals time to reach the ground from the maximum height