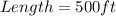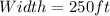Question

An elementary school is creating a rectangular garden on the side of the school building. The school has raised money to purchase 1000 feet of fence. In order to maximize the area they are using the building for one side and therefore need to use the fencing for the other three sides of the garden. Find the dimensions the school should use to maximize the area of the garden.

Answer 1

`Length = 500ft`

`Width = 250ft`

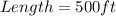
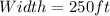
Explanation:

Given

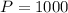`P = 1000` --- perimeter

Required

The dimensions that maximize the area

Let

`L \to Length`

`W \to Width`

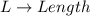
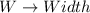
Such that:

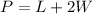`P = L + 2W` ---- Because one side is from the school building

This gives:

`L + 2W = 1000`

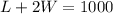
Make L the subject

`L = 1000 - 2W`

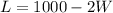
The area is then calculated as:

`A= L * W`

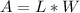
Substitute:
`L = 1000 - 2W`

`A= (1000 - 2W) * W`

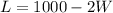
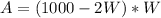
Open bracket, then set A to 0

`A = 1000W - 2W^2`

`1000W- 2W^2 = 0`

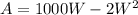
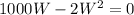
Rewrite as:

`-2W^2 + 1000W = 0`

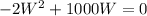
Assume the form of the above equation is:
`aW^2 + bW + c = 0`

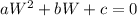
The value of W that maximizes it is:

`W = -(b)/(2a)`

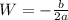
Where

`a = -2`

`b = 1000`

`c = 0`

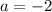
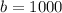
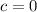
So:

`W = -(1000)/(2*-2)`

`W = (1000)/(2*2)`

`W = (1000)/(4)`

`W = 250`

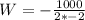
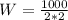
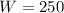
Recall that:

`L = 1000 - 2W`

`L =1000 - 2 * 250`

`L =1000 - 500`

`L = 500`

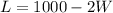
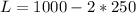
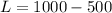
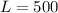
So, the dimensions that maximize the area is:

`Length = 500ft`

`Width = 250ft`