Question

Airlines must be careful about the total weight of baggage carried by a plane on a commercial flight. Passengers with items exceeding the maximum single-item weight (usually about 70 pounds) must pay a fee (usually about $50.00 per item). Airlines continually monitor the proportion of overweight items in order to evaluate the appropriateness of the overweight fees. English Air charges different amounts for overweight items on flights to the U.S. and Canada than it does on flights within Europe. Recently, a random sample of 256 items checked on English Air flights to the U.S. and Canada contained 37 overweight items, and an independent, random sample of 246 items checked on English Air flights within Europe contained 41 overweight items.

Based on these samples, can we conclude, at the 0.05 level of significance, that there is a difference between the proportion of all items on English Air flights to the U.S. and Canada which are overweight (p1) and the proportion of all items on English Air flights within Europe which are overweight (p2)?

Answer 1

The p-value of the test is 0.4966 > 0.05, which means that we cannot conclude, at the 0.05 level of significance, that there is a difference.

Explanation:

Before solving this question, we need to understand the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

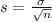For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
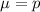`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

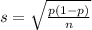
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

To US and Canada:

37 overweight out of 256. So

`p_1 = (37)/(256) = 0.1445, s_1 = \sqrt{(0.1445*0.8555)/(256)} = 0.022`

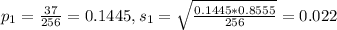
Europe:

41 overweight out of 246. So

`p_2 = (41)/(246) = 0.1667, s_2 = \sqrt{(0.1667*0.8333)/(246)} = 0.0238`

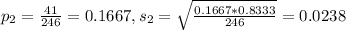
Test if there is a difference between the proportion of all items on English Air flights to the U.S. and Canada which are overweight (p1) and the proportion of all items on English Air flights within Europe which are overweight (p2):

At the null hypothesis, we test if there is no difference, that is, if the subtraction of the proportions is 0.

`H_0: p_1 - p_2 = 0`

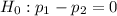
At the alternate hypothesis, we test if there is difference, that is, if the subtraction of the null hypothesis is different of 0.

`H_1: p_1 - p_2 \\eq 0`

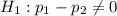
The test statistic is:

`z = (X - \mu)/(s)`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis and s is the standard error.

0 is tested at the null hypothesis:

This means that
`\mu = 0`

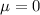
From the two samples:

`X = p_1 - p_2 = 0.1445 - 0.1667 = -0.0222`

`s = √(s_1^2+s_2^2) = √(0.022^2 + 0.0238^2) = 0.0324`

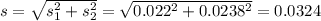
Value of the test statistic:

`z = (X - \mu)/(s)`

`z = (-0.0222 - 0)/(0.0324)`

`z = -0.68`

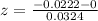
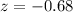
P-value of the test:

The p-value of the test is the probability of the sample proportion differing from 0 by at least 0.0222, which is P(|z| > 0.68), which is 2 multiplied by the p-value of z = -0.68.

Looking at the z-table, z = -0.68 has a p-value of 0.2483

0.2483*2 = 0.4966

The p-value of the test is 0.4966 > 0.05, which means that we cannot conclude, at the 0.05 level of significance, that there is a difference.