Question

Two disks are rotating about the same axis Disk A has a moment of inertia of 3.44 kg m2 and an angular velocity of 5.69 rad s Disk B is rotating with an angular velocity of 7.03 rad s The two disks are then linked together without the aid of any external torques so that they rotate as a single unit with an angular velocity of 4.23 rad s The axis of rotation for this unit is the same as that for the separate disks What is the moment of inertia of disk B

Answer 1

The moment of inertia of disk B is 0.446 kilogram-square meters.

Step-by-step explanation:

In this case, the moment of inertia of the disk B can be determined by means of the Principle of Conservation of Angular Momentum, whose model is:

`I_(A)\cdot \omega_(A) + I_(B)\cdot \omega_(B) = (I_(A) + I_(B))\cdot \omega` (1)

Where:

`I_(A)`,
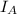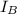`I_(B)` - Moments of inertia of disks A and B, in kilogram-square meters.

`\omega_(A)`,
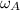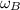`\omega_(B)` - Initial angular velocities of disks A and B, in radians per second.

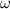`\omega` - Final angular velocity of the resulting system, in radians per second.

Let suppose that disk A rotates counterclockwise, whereas disk B rotates clockwise and that resulting system rotates counterclockwise. If we know that
`I_(A) = 3.44\,kg\cdot m^(2)`,
`\omega_(A) = 5.69\,(rad)/(s)`,
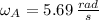`\omega_(B) = -7.03\,(rad)/(s)` and
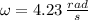`\omega = 4.23\,(rad)/(s)`, then the moment of inertia of the disk B is:

`I_(A) \cdot (\omega_(A) - \omega) = I_(B)\cdot (\omega - \omega_(B))`

`I_(B) = I_(A)\cdot \left((\omega_(A)-\omega)/(\omega - \omega_(B)) \right)`

`I_(B) = (3.44\,kg\cdot m^(2))\cdot \left((5.69\,(rad)/(s) - 4.23\,(rad)/(s) )/(4.23\,(rad)/(s) + 7.03\,(rad)/(s) ) \right)`

`I_(B) = 0.446\,kg\cdot m^(2)`

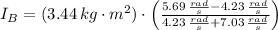
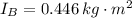
The moment of inertia of disk B is 0.446 kilogram-square meters.