Question

In the function f(x) = (x - 2)2 + 4, the minimum value occurs when x is​

Answer 1

x=2

Explanation:

The minimum value of the function would be its vertex, where the x-coordinate is defined as
`x=-(b)/(2a)` in the form of
`ax^2+bx+c=0`, so we expand the function first:

`f(x)=(x-2)^2+4\\\\f(x)=x^2-4x+4+4\\\\f(x)=x^2-4x+8`

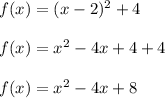
This is now in the form of
`ax^2+bx+c=0` and we use our rule:

`x=-(b)/(2a)\\ \\x=-(-4)/(2(1))\\ \\x=-(-4)/(2)\\ \\x=-(-2)\\\\x=2`

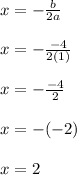
Thus, the minimum value of the function occurs when x=2