Question

Determine the area of the sector :

A circle with radius 12 inches formed by a central angle of 165°:

Round your answer to two decimal places.

______ inches squared

Answer 1

`\boxed {\boxed {\sf a \approx207.35 \ in^2}}`

Explanation:

Since the central angle is given in degrees, we should use this formula to find the area of the sector:

`a=(\theta)/(360) * \pi r^2`

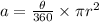
The central angle is 165 degrees and the radius is 12 inches.

• θ= 165
• r= 12 in

Substitute the values into the formula.

`a= (165)/(360) * \pi (12 \ in)^2`

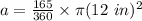
Solve the exponent.

• ( 12 in)² = 12 in * 12 in =144 in²

`a= (165)/(360) * \pi(144 \ in^2)`

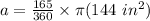
Multiply all the numbers together.

`a= 207.345115137 \ in^2`

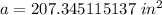
Round to the nearest hundredth (two decimal places).

• 207.345115137

The 5 in the thousandth place (in bold above) tells us to round the 4 in the hundredth place up to a 5.

`a \approx207.35 \ in^2`

The area of the sector is approximately 207.35 inches squared.