Question

Find the function y = f(t) passing through the point (0, 18) with the given first derivative.

dy/dt = 1/8 t

y = ?

Answer 1

`\displaystyle y = (t^2)/(16) + 18`

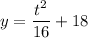
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Functions
• Function Notation
• Coordinates (x, y)

Calculus

Derivatives

Derivative Notation

Antiderivatives - Integrals

Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

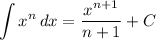
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

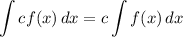
Explanation:

Step 1: Define

Identify

Point (0, 18)

`\displaystyle (dy)/(dt) = (1)/(8) t`

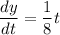
Step 2: Find General Solution

Use integration

1. [Derivative] Rewrite:
   `\displaystyle dy = (1)/(8) t\ dt`
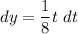
2. [Equality Property] Integrate both sides:
   `\displaystyle \int dy = \int {(1)/(8) t} \, dt`
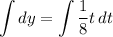
3. [Left Integral] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle y = \int {(1)/(8) t} \, dt`
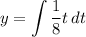
4. [Right Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle y = (1)/(8)\int {t} \, dt`
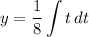
5. [Right Integral] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle y = (1)/(8)((t^2)/(2)) + C`
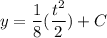
6. Multiply:
   `\displaystyle y = (t^2)/(16) + C`

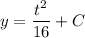
Step 3: Find Particular Solution

1. Substitute in point [Function]:
   `\displaystyle 18 = (0^2)/(16) + C`
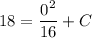
2. Simplify:
   `\displaystyle 18 = 0 + C`
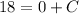
3. Add:
   `\displaystyle 18 = C`
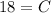
4. Rewrite:
   `\displaystyle C = 18`
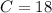
5. Substitute in C [Function]:
   `\displaystyle y = (t^2)/(16) + 18`

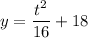
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integration

Book: College Calculus 10e