Question

Solve for K given in this equation

Answer 1

9514 1404 393

Answer:

logk(15) ≈ 0.902

k ≈ 57.6 or 12.8 or 20.1 depending on how you calculate it

Explanation:

The relevant rule of logarithms is ...

`\log_k(ab)=\log_k(a)+\log_k(b)`

__

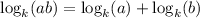
Using this rule, we have ...

`\log_k(15)=\log_k(3\cdot5)=\log_k(3)+\log_k(5)\\\\\log_k(15)=0.271+0.631\\\\ \boxed{\log_k(15)=0.902}`

_____

You will get different (inconsistent) results when you solve for k.

The applicable rule of logarithms is ...

`\log_k(a)=(\log(a))/(\log(k))`

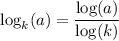
Then we can find log(k) and take the antilog to get ...

`\log(k)=(\log(a))/(\log_k(a))\\\\k=(10^(\log(3)))^(1/\log_k(3))=3^(1/0.271)\approx57.6\qquad\text{for $a=3$}\\\\ k=(10^(\log(5)))^(1/\log_k(5))=5^(1/0.631)\approx12.8\qquad\text{for $a=5$}\\\\ k=(10^(\log(15)))^(1/\log_k(15))=15^(1/0.902)\approx20.1\qquad\text{for $a=15$}`

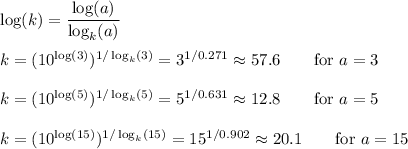
Here, we have used base-10 logarithms, but the same result is obtained for any base. The different results simply serve to show that the numbers in the problem are not self-consistent.