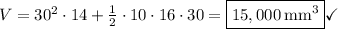Answer:
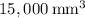
Explanation:
The composite figure consists of a square prism and a trapezoidal prism. By adding the volume of each, we obtain the volume of the composite figure.
The volume of the square prism is given by
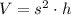 , where
, where
 is the base length and
is the base length and
 is the height. Substituting given values, we have:
is the height. Substituting given values, we have:
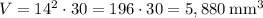
The volume of a trapezoidal prism is given by
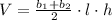 , where
, where
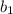 and
and
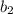 are bases of the trapezoid,
are bases of the trapezoid,
 is the length of the height of the trapezoid and
is the length of the height of the trapezoid and
 is the height. This may look very confusing, but to break it down, we're finding the area of the trapezoid (base) and multiplying it by the height. The area of a trapezoid is given by the average of the bases (
is the height. This may look very confusing, but to break it down, we're finding the area of the trapezoid (base) and multiplying it by the height. The area of a trapezoid is given by the average of the bases (
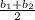 ) multiplied by the trapezoid's height (
) multiplied by the trapezoid's height (
 ).
).
Substituting given values, we get:
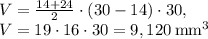
Therefore, the total volume of the composite figure is
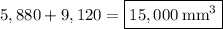 (ah, perfect)
(ah, perfect)
Alternatively, we can break the figure into a larger square prism and a triangular prism to verify the same answer: