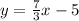Question

Please help me for this question

Answer 1

Mid-point:
`(0,-5)`

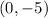
Equation:
`y=(7)/(3)x-5`

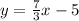
Explanation:

To find the mid-point of AB, simply add up their x and y coordinates and divide by 2 respectively to find their middle point.

`(\frac{{x__A}+{x__B}}{2},\frac{{y__A}+{y__B}}{2})`

`(\frac{{-7}+{7}}{2},\frac{{-2}+{(-8)}}{2})`

`(0,-5)`

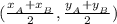
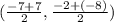
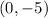
To find the perpendicular slope that passes through the mid-point, we need to know the slope between AB first.

Slope of AB:
`\frac{{y__2}-{y__1}}{{x__2}-{x__1}}` =
`\frac{{-8}-{-2)}}{{7}-{(-7)}}` =
`(-6)/(14)` =
`(-3)/(7)`

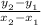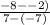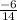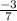
Multiplying slopes that are perpendicular with each other always results in -1.

`(-3)/(7)*m = -1`

`m=(7)/(3)`

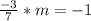
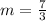
By the point slope form:

`({y}-{y__1})=m({x}-{x__1})`

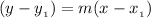
Plug in the coordinates of the mid-point:

`({y}-{(-5)})=(7)/(3) ({x}-{0})`

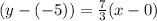
Equation:
`y=(7)/(3)x-5`