Answer:
The test statistic is t = 3.36.
Explanation:
You're testing the claim that the mean difference is greater than 0.7.
At the null hypothesis, we test if it is 0.7 or less, that is:
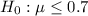
At the alternate hypothesis, we test if it is greater than 0.7, that is:
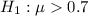
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
0.7 is tested at the null hypothesis:
This means that
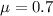
Survey of 35 people. From the sample, the mean difference was 0.95, with a standard deviation of 0.44.
This means that
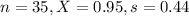
Calculate the test statistic

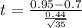
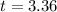
The test statistic is t = 3.36.