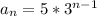Answer:
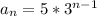
Explanation:
To find the nth term of a geometric sequence, you have the general formula:
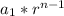
where a1 is the first term and r is the common ratio. In order to find the 4th term, we can substitute what we have(n is 4 because we are looking for the fourth term):
135 =
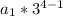
135 =

135 =
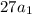
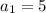
Now, we can substitute the first term back in: