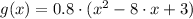Answer:
The rule to transform
 into
into
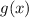 is:
is:
![g(x) = 0.8\cdot [f(x-7) - 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/23o3dfekvza51q7z0qa7wa30af6uxm9m89.png)
For
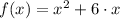 :
:

Explanation:
A vertical translation of a function is described by the following operation:
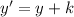 (1)
(1)
Where:
 - Original function.
- Original function.
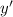 - Translated function.
- Translated function.
 - Vertical translation factor (
- Vertical translation factor (
 - Upwards)
- Upwards)
And a horizontal translation of a function is described by the following operation:
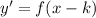 (2)
(2)
Where:
 - Independent variable.
- Independent variable.
 - Horizontal translation factor (
- Horizontal translation factor (
 - Rightwards)
- Rightwards)
And the dilation of a function is defined by this operation:
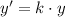 (3)
(3)
Where
 is the dilation factor (
is the dilation factor (
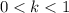 - Contraction)
- Contraction)
The rule to transform
 into
into
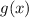 is:
is:
![g(x) = 0.8\cdot [f(x-7) - 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/23o3dfekvza51q7z0qa7wa30af6uxm9m89.png)
If we know that
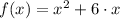 , then
, then
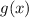 is:
is:
![g(x) = 0.8\cdot [(x-7)^(2)+6\cdot (x-7) - 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/t4u7paqxhkyy52a3jgsy965r58otzaq78v.png)
![g(x) = 0.8\cdot [(x^(2)-14\cdot x + 49)+(6\cdot x -42) - 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/31qh925joluafzityvv3am8fy8mbn35seo.png)