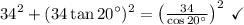Question

Can you help me to solve this

Using special right triangles and for the other using trigonometry

Answer 1

`\text{Triangle 1:}\\\\x=30√(2),\\\\\text{Triangle 2:}\\x\approx 36.18,\\?\approx12.37`

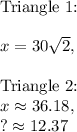
Explanation:

*Notes (clarified by the person who asked this question):

-The triangle on the right has a right angle (angle that appears to be a right angle is a right angle)

-The bottom side of the right triangle is marked with a question mark (?)

Triangle 1 (triangle on left):

Special triangles:

In all 45-45-90 triangles, the ratio of the sides is
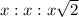`x:x:x√(2)`, where
`x√(2)` is the hypotenuse of the triangle. Since one of the legs is marked as
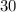`30`, the hypotenuse must be
`\boxed{30√(2)}`

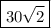
It's also possible to use a variety of trigonometry to solve this problem. Basic trig for right triangles is applicable and may be the simplest:

`\cos 45^(\circ)=(30)/(x),\\x=(30)/(\cos 45^(\circ))=(30)/((√(2))/(2))=30\cdot (2)/(√(2))=(60)/(√(2))=(60\cdot√(2))/(√(2)\cdot √(2))=(60√(2))/(2)=\boxed{30√(2)}\\`

Triangle 2 (triangle on right):

We can use basic trig for right triangles to set up the following equations:

`\cos 20^(\circ)=(34)/(x),\\x=(34)/(\cos 20^(\circ))\approx \boxed{36.18}`,

`\tan 20^(\circ)=(?)/(34),\\?=34\tan 20^(\circ)\approx \boxed{12.37}`

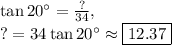
We can verify these answers using the Pythagorean theorem. The Pythagorean theorem states that in all right triangles, the following must be true:

`a^2+b^2=c^2`, where
`c` is the hypotenuse of the triangle and
`a` and
`b` are two legs of the triangle.

Verify
`34^2+(34\tan20^(\circ))^2=\left((34)/(\cos20^(\circ))\right)^2\:\checkmark`