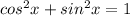Answer:
Identity (a) can be re-written as
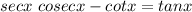
which we already proven in another question, while for idenity (b)
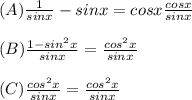
step A is simply expressing each function in terms of sine and cosine.
step B is adding the terms on the LHS while multiplying the one on RHS.
step C is replacing the term on the numerator with the equivalent from the pithagorean identity