Question

A market research team thinks that their new ad campaign is better than their old one. They used to be able to sell to 50% of those who saw their ads. To test their thought, they will run a hypothesis test. They take a random sample of 100 potential buyers and find that they convinced 60 of these people to buy their product. The test will be run at a 1% significance level.

a. The test statistic is 2 and we conclude that the new ad campaign is not signficantly better.
b. The test statistic is 2 and we conclude that the new ad campaign is signficantly better.
c. The test stat is 2.236 and we conclude that the new ad campaign is not significantly better.
d. The test stat is 2.236 and we conclude that the new ad campaign is significantly better.
e. The test stat is 2.5 and we are left with a test that is inconclusive.

Answer 1

a. The test statistic is 2 and we conclude that the new ad campaign is not signficantly better.

Explanation:

They used to be able to sell to 50% of those who saw their ads. Test if the new campaign is better.

At the null hypothesis, we test is it is the same, that is, the proportion is the same.

`H_0: p = 0.5`

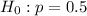
At the alternate hypothesis, we test if it is significantly better, that is, the proportion is above 50%.

`H_1: p > 0.5`

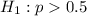
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.5 is tested at the null hypothesis:

This means that
`\mu = 0.5, \sigma = √(0.5*0.5) = 0.5`

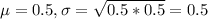
They take a random sample of 100 potential buyers and find that they convinced 60 of these people to buy their product.

This means that
`n = 100, X = (60)/(100) = 0.6`

Test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.6 - 0.5)/((0.5)/(√(100)))`

`z = 2`

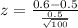
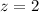
The test statistic is 2.

P-value of the test and decision:

The p-value of the test is the probability of finding a sample proportion above 0.6, which is 1 subtracted the by p-value of z = 2.

Looking at the z-table, z = 2 has a p-value of 0.9772.

1 - 0.9772 = 0.0228.

The p-value of the test is 0.0228 > 0.01, which means that we cannot conclude that the new ad campaign is signficantly better, so the correct answer is given by option A.