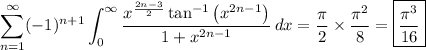Substitute
 and
and
 . Then the integral is
. Then the integral is

which is to say, the integral is now independent of n. Then
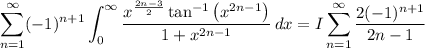
Let's evaluate the sum. Recall that if |x| < 1, we have
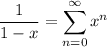
which means
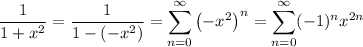
By the fundamental theorem of calculus, integrating both sides gives
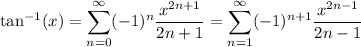
As x approaches 1 from below, we have
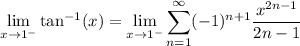
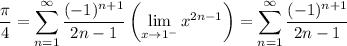
and so
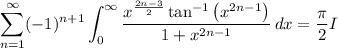
Now compute the remaining integral. First split it at y = 1 :
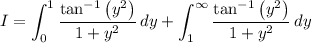
In the second integral, notice that replacing
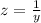 and
and
 yields
yields
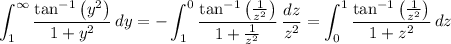
The inverse tangent function has the property
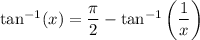
so it follows that
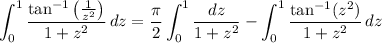
and hence
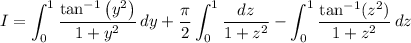
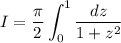
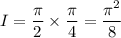
Then the original expression has an exact value of