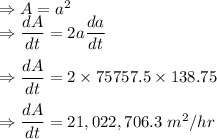Answer:
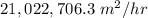
Explanation:
Given
The rate of change of perimeter of a square is increasing at a rate of
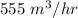
At a certain instant, the perimeter is
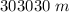
At this instant side of square is
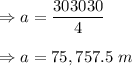
Rate of change of perimeter is
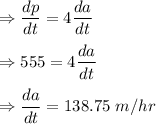
At this instant, rate of change of the area of the square is