Question

Please help and show the formula used, along with all substitutions and calculations needed

Answer 1

The given triangle is right.

Explanation:

The Pythagorean converse theorem states the following: if one can substitute the sides of a triangle into the following formula:

`a^2+b^2=c^2`

If the equation formed is a true statement, then the triangle is right, if it is not, then the triangle is not right. In this case, one is not given the angle that has the right angle, however, the hypotenuse is the longest side in a right triangle. Therefore, if the triangle is right, then the hypotenuse is the longest, then side (c) is the longest side in the given triangle. Then side (a) and (b) are the legs, the sides adjacent to the right angle. It doesn't matter which sides one substitutes for these parameters.

Substitute in the given values and solve to prove the triangle is right,

`a^2+b^2=c^2\\`

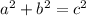
Substitute,

`(9.6)^2+(12.8)^2=(16)^2`

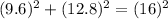
Simplify,

`92.16+163.84=256`

`256=256`

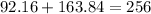
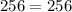
The given triangle is right since its sides follow the Pythagorean converse theorem.