Solution :
Cost
Destination Destination Destination Maximum supply
Origin 1 5 7 600
Origin 2 10 10 800
15, for > 200 15, for > 200
Demand 500 700
Variables
Destination 1 2
Origin 1
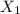
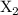
Origin 2
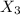
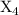
Constraints :
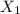 ,
,
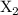 ,
,
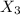 ,
,
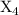 ≥ 0
≥ 0
Supply :
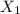 +
+
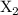 ≤ 600
≤ 600
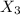 +
+
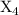 ≤ 800
≤ 800
Demand :
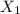 +
+
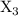 ≥ 500
≥ 500
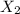 +
+
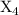 ≥ 700
≥ 700
Objective function :
Min z =
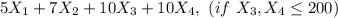
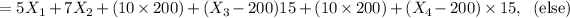
Costs :
Destination 1 Destination 2
Origin 1 5 7
Origin 2 10 10
15 15
Variables :
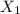
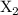
300 300
200 400
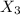
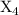
Objective function : Min z = 10600
Constraints:
Supply 600 ≤ 600
600 ≤ 800
Demand 500 ≥ 500
700 ≥ 500
Therefore, the total cost is 10,600.