Question

A researcher wants to test if the mean annual salary of all lawyers in a city is different from $110,000. A random sample of 50 lawyers selected from the city reveals a mean annual salary of $ 112000, Assume that σ-$16 100, and that the test is to be made at the 2% significance level What are the critical values of z?

2.33 and 2.33
2.05 and 2.05
-1.645 and 1.645
-1.28 and 1.28
What is the value of the test statistic, z, rounded to three decimal places?
What is the p-value for this hypothesis test, rounded to four decimal places?
Should you reject or fail to reject the null hypothesis in this test?

Answer 1

This is the two tailed test.

The null hypothesis and the alternate hypothesis is as :

Null hypothesis is
`$H_0:\mu=110000$`

Alternate hypothesis is
`$H_0:\mu \\eq110000$`

`$\overline x = 112000, \ \mu = 110000, \sigma = 16100, n = 50, \alpha = 0.02$`

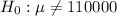
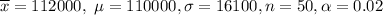
Therefore, the critical value of z is :

`$z_(\alpha) = -2.33 \text{ and}\ 2.33$`

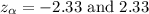
Now the test statics is :

`$z=(((\overline x - \mu))/(\sigma))/(\sqrt n)$`

`$z=\frac{((112000-110000))/(16100)}{\sqrt {50}}$`

`$z=0.87$`

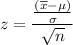
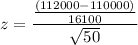
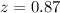
The test statics is 0.878

We see that it is a right tailed test.

`$P(z > 0.878)=1-P(z<0.878) = 1 - 0.81 = 0.19$`

`$P- \text{value}= \ 2 * 0.19$`

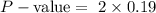
= 0.3800

Thus , P-value > α

So we fail to reject the null hypothesis.