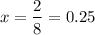Question

Consumers know that some fraction x of all new cars produced and sold in the market are defective. The defective ones cannot be identified except by those who own them. Cars do not depreciate with use. Consumers are risk-neutral and value nondefective cars at $10,000 each. New cars sell for $8,000 and used ones for $2,000. (Note that since buyers are risk-neutral, the price of a new car reflects the expected value of purchasing a car that may or may not be defective.)What is the fraction x?Instructions: Enter x as a number rounded to two decimal places. For example, if x = 1/3 enter 0.33.

Answer 1

0.25

Step-by-step explanation:

Given :

The
`$\text{consumers value}$` the non defective cars =
`$\$ 10,000$`

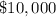
We will consider all the defective
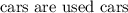`$\text{ cars are used cars}$` only. This is only because the value of the used car is $ 2000 and it is lower than the price of a good car that is $10,000. Thus only defective cars are being sold as the old cars.

For a risk neutral customer, the price that he is ready to give for the new car is the reservation price of a non defective car. It means that (the amount of $ 8000 is the value of the good car x chances of getting a good car) +( the value of the bad car x chances of getting a bad car).

Since we know that x is the fraction of all the cars sold in the market are defective, it means that the fraction of the good cars is 1 - x. Thus putting the values,

`$x* 2000+(1-x)* 10000=8000$`

`$10000-8000x=80000$`

`$8000x=2000$`

`$x=(2)/(8)$`

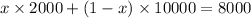
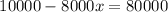
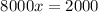
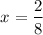
= 0.25

Thus the value of :

`$x=(2)/(8) = 0.25$`