Question

Each time a component is tested the trial is a success (S) or failure (F). Suppose the component is tested repeatedly until a success occurs on three consecutive trials. Let Y denote the number of trials necessary to achieve this. List all outcomes corresponding to the five smallest possile values of Y, and state which Y value is associated with each one.

Y Outcomes
3
4
5
6
7

Answer 1

`(a)\ \{SSS\}`

`(b)\ \{FSSS\}`

`(c)\ \{FFSSS, SFSSS\}`

`(d)\ \{FFFSSS, SSFSSS, SFFSSS, FSFSSS\}`

`(e)\ \{FFFFSSS, FFSFSSS, FSSFSSS, SSFFSSS, SFSFSSS, SFFFSSS, FSFFSSS\}`

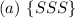
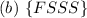
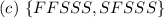
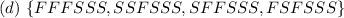
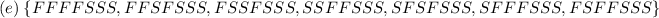
Explanation:

Given

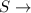`S\to` Success

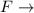`F\to` Failure

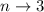`n \to 3` Consecutive trials until S happens

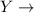`Y \to` Number of trials

For every possible outcome, the last 3 must be SSS. So, we have:

`(a)\ Y = 3`

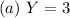
The only possibility here is:
`\{SSS\}`

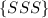
because 3 trials implies that all outcomes must be S.

`(b)\ Y = 4`

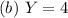
The only possibility here is:

`\{FSSS\}`

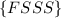
because 4 trials implies that the first outcome must be F

`(c)\ Y = 5`

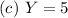
The possibilities are:

`\{FFSSS, SFSSS\}`

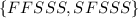
because 5 trials implies that the first and the second outcomes must be FS or SF.

`(d)\ Y = 6`

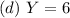
The possibilities are:

`\{FFFSSS, SSFSSS, SFFSSS, FSFSSS\}`

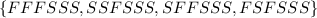
because 6 trials implies that the first three outcomes are: FFF, SSF and SFF

`(e)\ Y = 7`

The possibilities are:

`\{FFFFSSS, FFSFSSS, FSSFSSS, SSFFSSS, SFSFSSS, SFFFSSS, FSFFSSS\}`

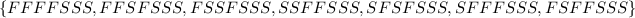
because 7 trials implies that the first three outcomes are: FFFF, FSSF and SSFF and FFSF (similar to (e))