Answer:
a) The model for the sales of Garmin is represented by
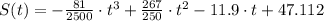 .
.
b) The average sales of Garmin from 2008 through 2013 were $ 2.5 billion.
Explanation:
a) The model for the sales of Garmin is obtained by integration:
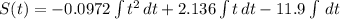
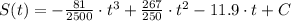 (1)
(1)
Where
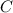 is the integration constant.
is the integration constant.
If we know that
 and
and
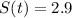 , then the model for the sales of Garmin is:
, then the model for the sales of Garmin is:
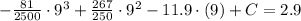
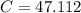
The model for the sales of Garmin is represented by
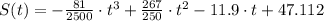 .
.
b) The average sales of the Garmin from 2008 through 2013 (
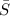 ) is determined by the integral form of the definition of average, this is:
) is determined by the integral form of the definition of average, this is:
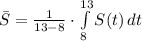 (2)
(2)
![\bar S = (1)/(5)\cdot \int\limits^(13)_(8) {\left[-(81)/(2500)\cdot t^(3) + (267)/(250)\cdot t^(2)-11.9\cdot t + 47.112 \right]} \, dt](https://img.qammunity.org/2022/formulas/mathematics/college/cokq0tzz33oi10s4hg2q746uxjqh2udfsz.png)
![\bar S = (1)/(5)\cdot \left[-(81)/(10000)\cdot (13^(4)-8^(4)) +(89)/(250)\cdot (13^(3)-8^(3)) -(119)/(20)\cdot (13^(2)-8^(2)) +47.112\cdot (13-8) \right]](https://img.qammunity.org/2022/formulas/mathematics/college/qtyoqk4ug2pfb3bfj6c7tgd2y41azk83ld.png)
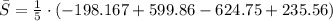
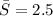
The average sales of Garmin from 2008 through 2013 were $ 2.5 billion.