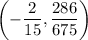Answer:
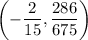
Explanation:
to figure out the infection point
take derivative both sides:
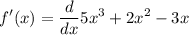
By sum derivation rule we acquire:
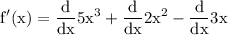
apply exponent derivation rule which yields:
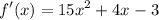
take derivative in both sides once again which yields:

remember that, derivative of a constant is always 0 so,
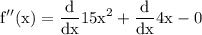
by exponent derivation rule we acquire:
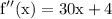
substitute f''(x) to 0 figure out the x coordinate of the inflection point:
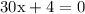
cancel 4 from both sides:
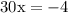
divide both sides by 30:
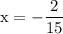
now plugin the value of x to the given function to figure out the y coordinate of the inflection point:
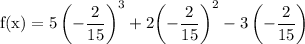
By simplifying we acquire:
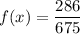
hence,
the coordinates of inflection point are