Answer:
The answer is "
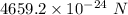 "
"
Step-by-step explanation:
The magnetic field at ehe mid point of the coils is,
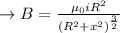
Here, i is the current through the loop, R is the radius of the loop and x is the distance of the midpoint from the loop.
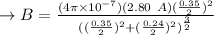
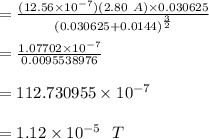
Calculating the force experienced through the protons:
